Tolerance Stack-Up Analysis: Ensuring Precision in Mechanical Assemblies

Manufacturing parts without considering tolerance stack-up can result in assemblies that don't fit together or function as intended. Overly tight tolerances can increase manufacturing costs and lead to higher rejection rates, while overly loose tolerances can compromise product performance. Tolerance stack-up analysis allows engineers to balance these factors by:

Ensuring assemblies meet functional requirements.
Reducing manufacturing costs by optimizing tolerances.
Minimizing the risk of assembly issues and product failures.

Several methods are used to perform tolerance stack-up analysis, each with its own advantages and applications:

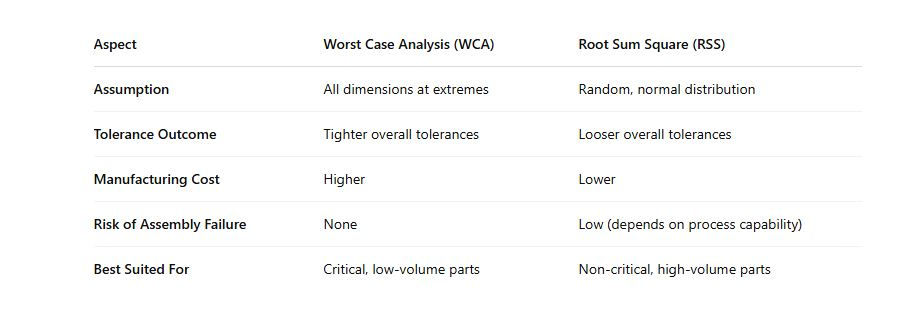
1. Worst-Case Analysis (WCA)

WCA assumes that all parts are at their maximum or minimum tolerance limits simultaneously. This method ensures 100% interchangeability and is suitable for critical assemblies where failure is not an option. However, it often leads to very tight tolerances, increasing manufacturing costs.

2. Root Sum Square (RSS) Analysis

RSS is a statistical method that assumes tolerances are random and independent, following a normal distribution. It calculates the square root of the sum of the squares of individual tolerances, providing a more realistic estimate of variation in mass production. RSS allows for looser tolerances compared to WCA, reducing costs while maintaining acceptable quality levels.

3. Monte Carlo Analysis

Monte Carlo analysis uses random sampling and statistical modeling to simulate the assembly process thousands of times. It accounts for complex interactions and non-linear relationships between components, providing a comprehensive understanding of potential variations. This method is beneficial for complex assemblies and when dealing with non-normal distributions.

Example:

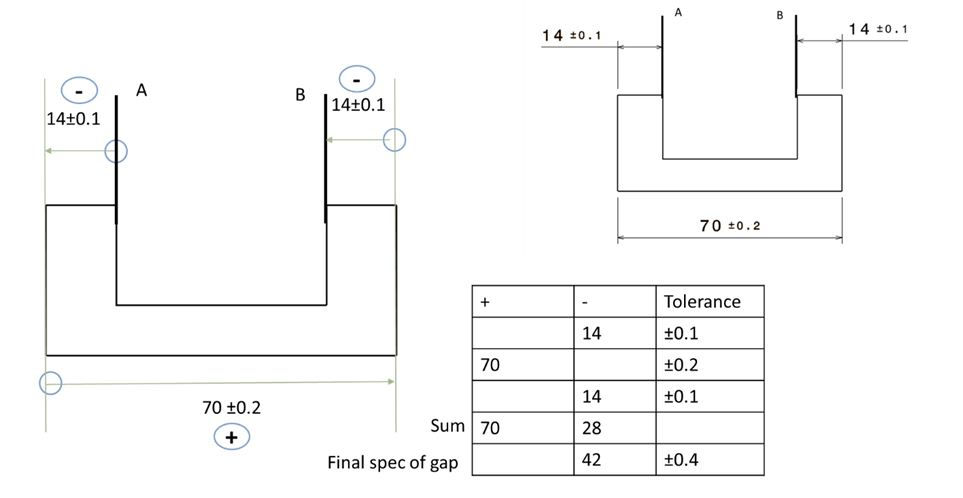
Let's consider this with an example by solving through worst-case analysis.

The general steps for worst-case analysis are:

Label the distance to be studied A-B
1. Positive and negative directions are set
Left to Right is positive
Right to left is negative
Develop a loop diagram starting from A to B
Start from A and move towards B through the Loop
The dimensions in the positive direction are added together, and the dimensions in the negative are added together
The negative dimensions sum is subtracted from the positive direction sum.
All tolerances are added together. The total added tolerance is the possible allowed variation for the distance being studied
Loop Diagram with the tolerance analysis table:

Let's solve the same through the RSS Method:

Total RSS Tolerance=√ (T1)2+(T2)2+⋯+(Tn)2

Calculate the square root of the sum of the squares of individual tolerances:

√(0.1)² +(0.2)² + (0.1)² = √0.01 + 0.04 + 0.01

= √0.06

= 0.24

Total tolerance= 42 +/- 0.24

This example illustrates that RSS provides a narrower tolerance range compared to WCA, allowing for more flexibility in individual component tolerances while still achieving the desired assembly specifications.

Comparison of WCA and RSS Method:

WCA ensures absolute reliability by considering the most extreme scenarios, which often leads to overly tight component tolerances and higher production costs. In contrast, the RSS method offers a more balanced approach, accepting minimal risk for greater manufacturing efficiency. The choice between these methods should be guided by the criticality of the assembly, acceptable risk levels, and cost considerations.

Comparing RSS and Worst Case Analysis (WCA)

Best Practices for Tolerance Stack-Up Analysis

Define critical-to-function dimensions early.
Choose the analysis method based on design context and production volume.
Use CAD tools that support tolerance analysis simulations.
Incorporate real production data to refine models.
Document assumptions used in the analysis for future reference.

Tolerance stack-up analysis is a vital aspect of mechanical design, ensuring that assemblies function correctly while optimizing manufacturing costs. By understanding and applying appropriate analysis methods, Worst-Case, RSS, or Monte Carlo, engineers can make informed decisions tailored to the specific requirements and complexities of their designs. Selecting the right method depends on factors such as production volume, assembly complexity, and acceptable risk levels.